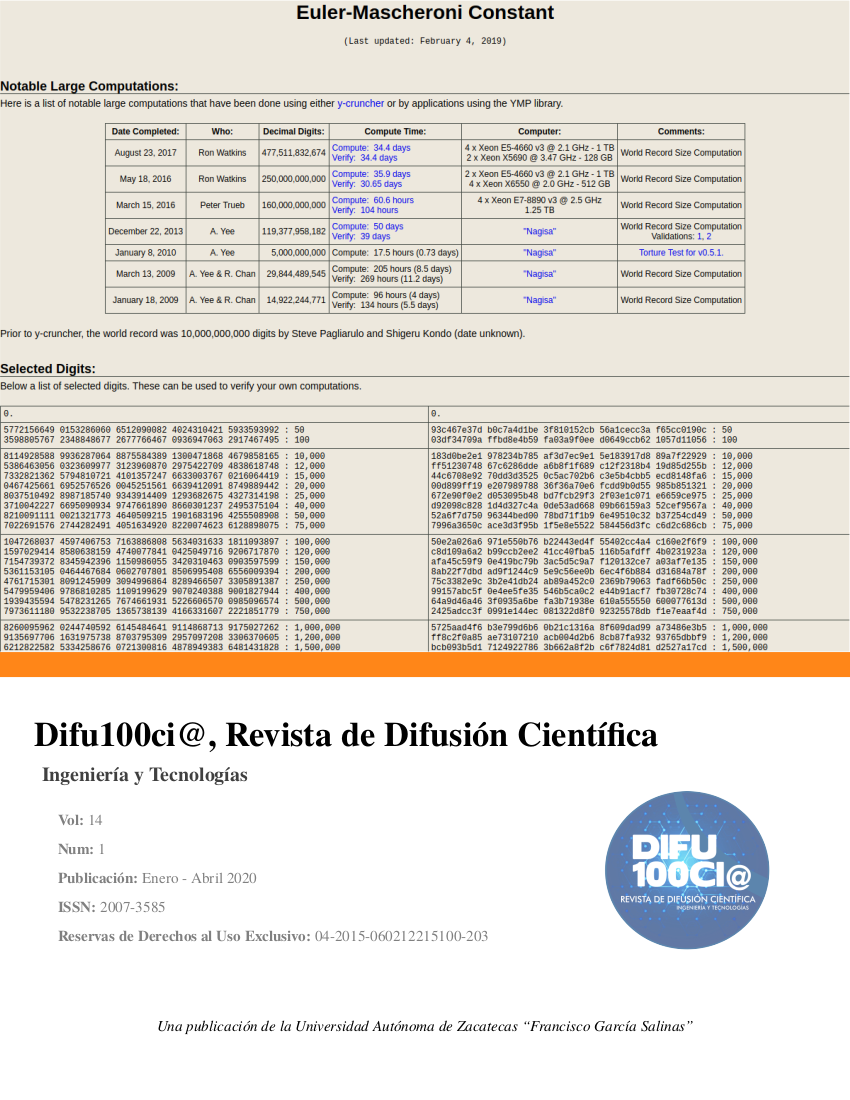
A computer based approach for harmonic numbers calculation and a numerical growth rate

Resumen

Some computational limitations when it is intended to calculate harmonic numbers for very large n values are
analyzed. A reformulation of Euler’s theorem is proposed, with which the range of its numerical calculation is
extended. Two interesting results are reported, in the first one, an approximate grow rate ∆H = 2.3026 /decade is
defined, which follows immediately from Euler’s theorem. In the second, for n = 10 p , where p can be as large as
p = 10 307 , it is proposed H n to be H n ≈ M p + γ , i.e., p = log(n) times a constant M (plus γ ), which is also given,
and log is the base 10 logarithm.